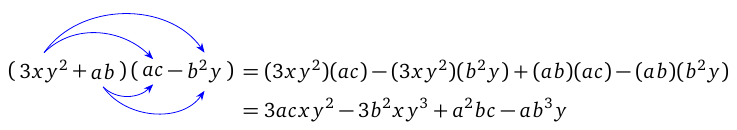Polynomials
Definition
- A polynomial is an expression made of terms with positive integer exponents only. For example, all the following are polynomials. \[\begin{aligned} & 7;\qquad && x^2;\qquad && 8k \\ & n;\qquad && m^3;\qquad && a^2b^3 \\ & x-5;\qquad && 2x+3y;\qquad && 3x^2-2y^3 \\ & a^2b+3ab^3-4xy;\qquad && \dfrac{cd^2}{7};\qquad && \dfrac{m}{\sqrt{5}} \end{aligned}\]
- No division by variables is allowed in a polynomial term, because division is equivalent to negative exponents.
- No roots of variables are allowed in polynomial terms, because these are allowed to rational exponents.
For instance, the following are not polynomials.
\[\begin{aligned}
& \dfrac{3}{x};\qquad && a^{-2};\qquad && b^{\frac{2}{3}} \\
& \dfrac{a}{b-2};\qquad && \sqrt{x};\qquad && \dfrac{x^2-1}{x} \\
& \sqrt{m^2+5};\qquad && k^3-\dfrac{3}{n}
\end{aligned}\]
- The degree of a polynomial is the highest degree of its terms. We typically write the terms of a polynomial in a descending order of their degree.
Terminology
A polynomial is named according to its degree as follows.
| Degree | Name |
|---|---|
| 1 | Linear |
| 2 | Quadratic |
| 3 | Cubic |
| 4 | Quartic |
The general term ‘\(n\)-degree’ polynomial applies to any polynomial of degree \(n\).
Distributive property
When we multiply a monomial by a polynomial, we multiply it by each term in the polynomial. We say that multiplication is distributive over addition and subtraction.
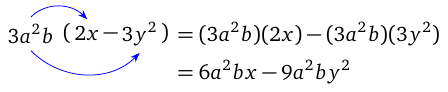
When we multiply a polynomial by another, we multiply each term in the first by each term in the second. In case of a binomial multiplied by another binomial, we have the acronym ‘FOIL’, which stands for ‘First’, ‘Outer’, ‘Inner’, and ‘Last’.
