Angle bisectors and incentre

An angle bisector of a triangle is the line that passes through a vertex and bisects (divides into equal halves) the angle at that vertex. All three angle bisectors intersect at one and the same point, called the incentre of the triangle. The incentre is the centre of the inscribed circle, which is the circle that is tangent (i.e., only ‘touches’) all three sides of the triangle from the inside.

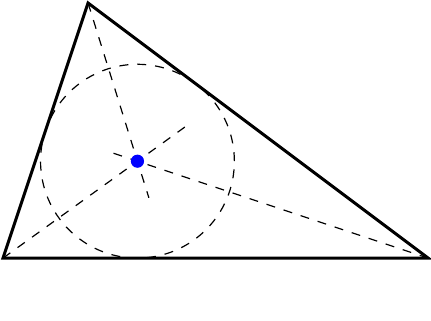
Angle bisector and incentre - acute triangle

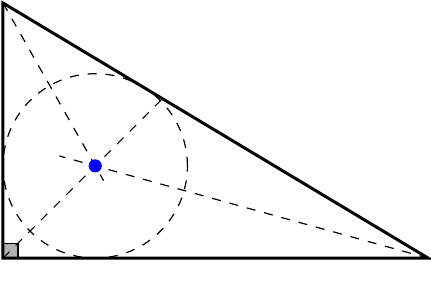
Angle bisector and incentre - right triangle

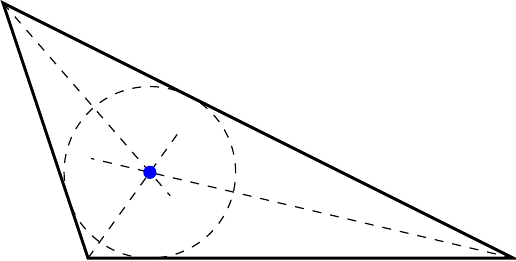
Theorems of angle bisectors and incentre

The incentre, being the radius of the inscribed circle, is at the same distance from all three sides of a triangle.

$Distance from incentre to sides$
An angle bisector divides the side of a triangle into two segments. The ratio of the lengths of these segments is equal to the ratio of their adjacent triangle sides.

$Angle bisector theorem (1)$

\[\dfrac{\color{blue}{AD}}{\color{red}{BD}}=\dfrac{\color{blue}{AC}}{\color{red}{BC}}\]
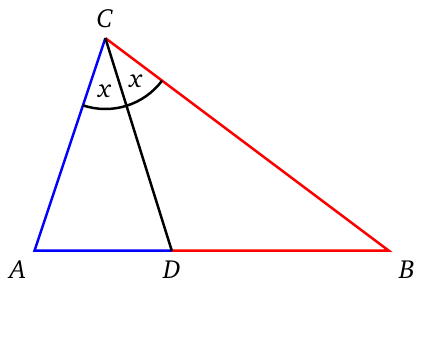
If the exterior angle bisector of the exterior angle at $C$ intersects the extension of $AB$ at $D$, then \[\dfrac{AD}{BD}=\dfrac{AC}{BC}\]

$Angle bisector theorem (2)$
In a triangle that is not isosceles, all three exterior angle bisectors intersect the extensions of the sides, and those points of intersection lie on the same line.