Triangles
- Medians and centroid
- Altitudes and orthocentre
- Right bisectors and circumcentre
- Angle bisectors and incentre
- Special triangles
كتاب روابط اجتياز لـ Triangles
Triangle terminology
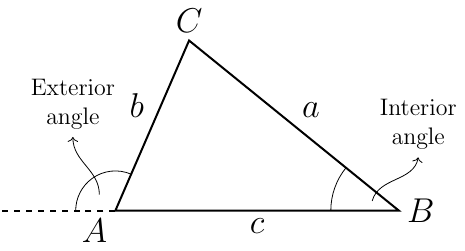
A triangle is composed of three segments, called sides, connected to each other at their end points, called vertices (plural of vertex). Vertices are usually given uppercase letters, while sides (and also side lengths) are given lowercase letters. Each side is given a matching letter to the vertex opposite to it. Sides connected to each other by a common point are called adjacent sides. Angles inside a triangle are called interior angles. The angle between a side and the extension of an adjacent side is called an exterior angle.
Classification by interior angles
- Acute triangle: all interior angles are acute.
- Right triangle: one interior angle is a right angle.
- Obtuse triangle: one interior angle is an obtuse angle.
Classification by side length
- Scalene triangle: no side is equal to another.
- Isosceles triangle: two sides are equal to one another.
- Equilateral triangle: all three sides are equal to one another.
| Acute | Right | Obtuse | |
|---|---|---|---|
| Scalene |
|
|
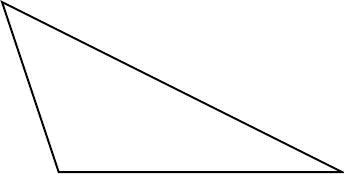
|
| Isosceles |
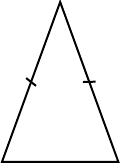
|
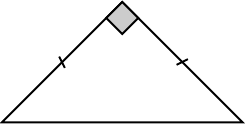
|
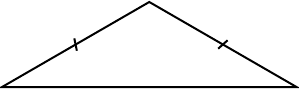
|
| Equilateral |
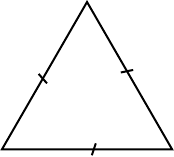
|
Not possible | Not possible |
Triangle theorems
The sum of the interior angles of a triangle is \(180^\circ\).
\[\angle A+\angle B+\angle C=180^\circ\]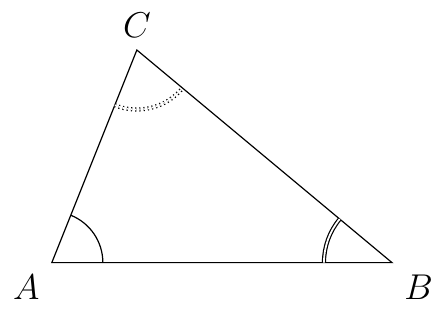
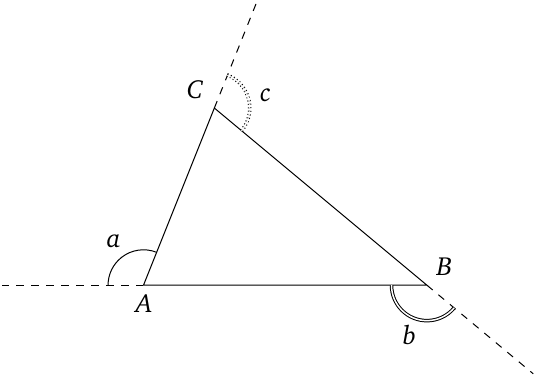
An exterior angle is equal to the sum of the two interior, non-adjacent angles.
\begin{align} \angle a &= \angle ABC + \angle BCA \\ \angle b &= \angle BAC + \angle BCA \\ \angle c &= \angle BAC + \angle ABC \end{align}The sum of the exterior angles of a triangle is \(360^\circ\).
\[\angle a+\angle b+\angle c=360^\circ\]