Uniform motion
Book traversal links for Uniform motion
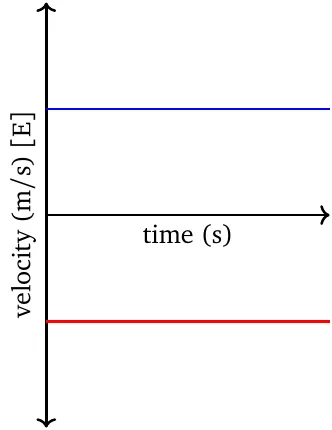
In uniform motion, velocity is constant. This means that both the magnitude of velocity (i.e., the speed) and the direction of motion remain the same throughout the motion. Because of this, average and instantaneous velocity are the same throughout the motion, and we have one and only one equation.
\[\vec{v}=\dfrac{\Delta\vec{d}}{\Delta t}\]There is a total of 3 parameters: \(\vec{v}\), \(\Delta\vec{d}\) and \(\Delta t\). We need to know 2 parameters in order to calculate the third.
In the displacement-time graph, the relation is always linear. The slope (i.e., velocity) is zero if and only if the object is stationary.
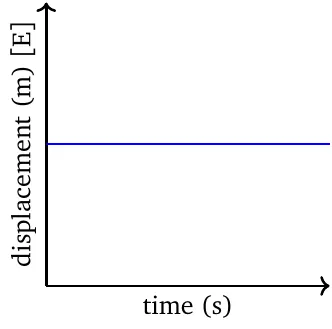
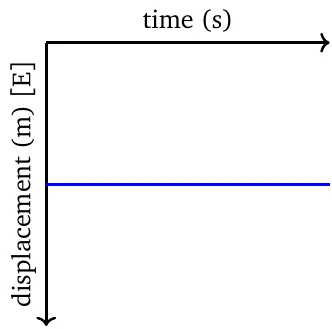
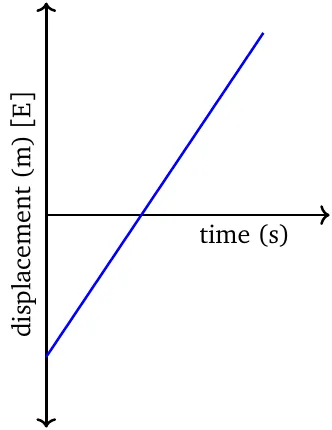
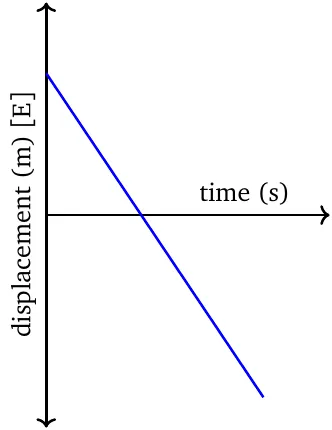
In the displacement-time graph, the slope is positive if and only if the object is moving in the positive direction, and is negative if and only if the object is moving in the negative direction.
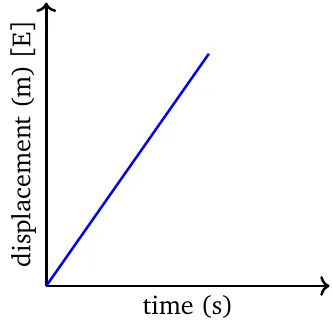
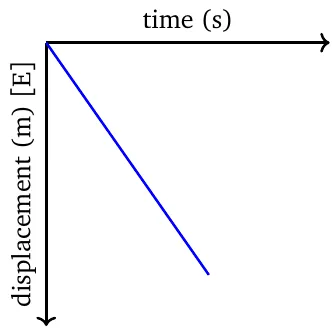
The \(\boldsymbol{y}\)-intercept is the point where the object starts moving. The origin of coordinates is the reference point.
In the velocity-time graph, the relation is always a horizontal line.