Uniform acceleration

In uniform acceleration, the constant parameter is acceleration. It follows that velocity must change, either in magnitude or in direction. At this level, we only consider when the magnitude of velocity changes. This kind of motion (as well as uniform motion) is called rectilinear motion; i.e., motion in a straight line.

Because velocity changes and acceleration is not zero, we have 5 parameters: \(\vec{a}\), \(\vec{v}_i\), \(\vec{v}_f\), \(\Delta\vec{d}\) and \(\Delta t\). In order to calculate the missing parameters, we need to know 3 parameters. We have 5 equations to choose from; each of which is missing one of the 5 parameters.

\begin{align} \vec{v}_f &= \vec{v}_i + \vec{a}\Delta t \tag{missing \(\Delta\vec{d}\)} \\ \Delta\vec{d} &= \vec{v}_i\Delta t + \tfrac{1}{2}\vec{a}(\Delta t)^2 \tag{missing \(\vec{v}_f\)} \\ \Delta\vec{d} &= \vec{v}_f\Delta t - \tfrac{1}{2}\vec{a}(\Delta t)^2 \tag{missing \(\vec{v}_i\)} \\ \Delta\vec{d} &= \tfrac{1}{2}(\vec{v}_i + \vec{v}_f)\Delta t \tag{missing \(\vec{a}\)} \\ v_f^2 &= v_i^2 + 2a\Delta d \tag{missing \(\Delta t\)} \end{align}

In these equations, velocity and acceleration are instantaneous values, not average. The first four equations are vector equations, while the last one is a scalar equation; hence interpreting results from the last one should be done with care.

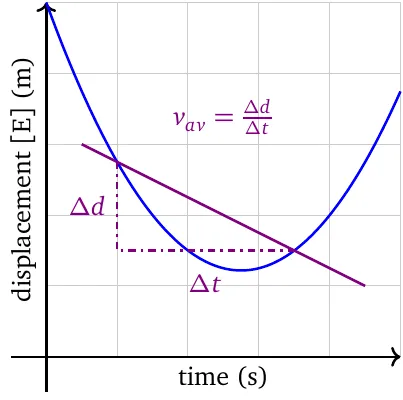
Note that average velocity and average acceleration are calculated as follows.

\[\vec{v}_{\text{av}}=\dfrac{\Delta\vec{d}}{\Delta t};\qquad\qquad\vec{a}_{\text{av}}=\dfrac{\Delta\vec{v}}{\Delta t}\]

The average rate of change is the slope of the secant line. The sign of the slope is the direction of the rate of change.

Figure 1. Average velocity is the slope of the secant in the displacement-time graph.

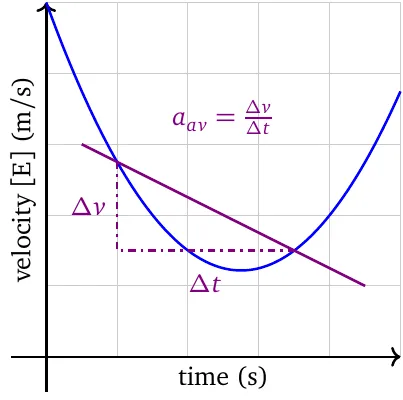
Figure 2. Average acceleration is the slope of the secant in the velocity-time graph.

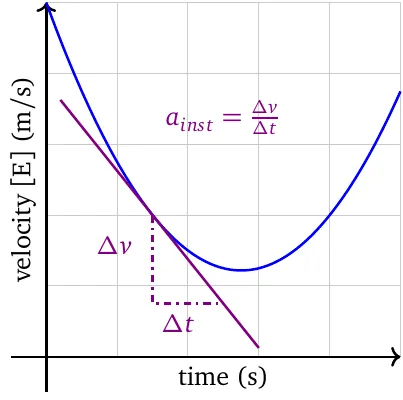
The instantaneous rate of change is the slope of the tangent line. The sign of the slope is the direction of the rate of change.

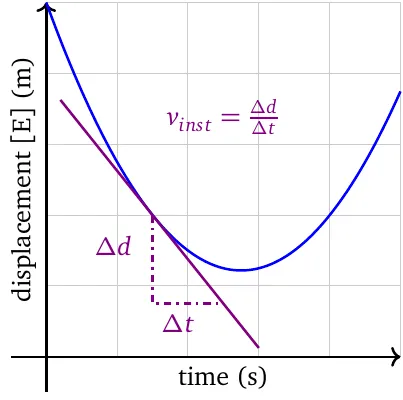
Figure 3. Instantaneous velocity is the slope of the tangent in the displacement-time graph.

Figure 4. Instantaneous acceleration is the slope of the tangent in the velocity-time graph.

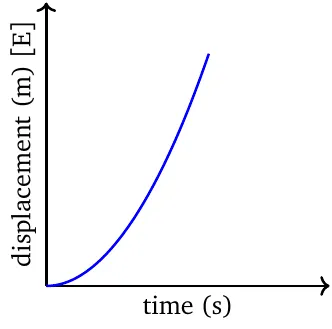
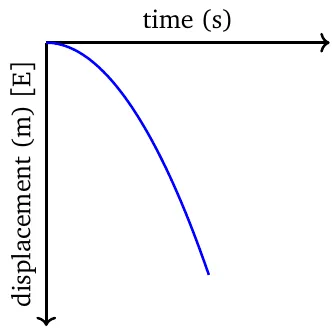
The displacement-time graph in uniform acceleration is always parabolic. It ‘opens up’ when acceleration is in the positive direction, and ‘opens down’ when acceleration is in the negative direction.

D-T graph - positive acceleration — Figure 5. Displacement-time graph with acceleration in the positive direction (eastward in this case).

D-T graph - negative acceleration — Figure 6. Displacement-time graph with acceleration in the negative direction (westward in this case).

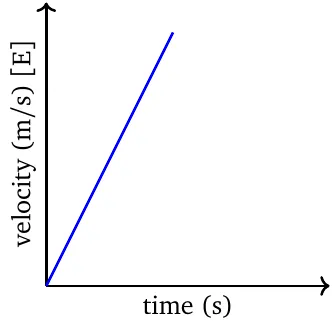
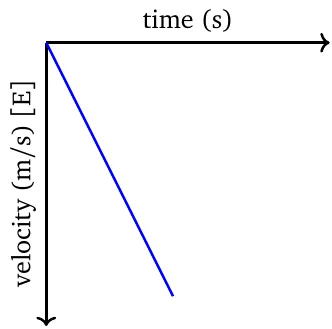
The velocity-time graph in uniform acceleration is always linear. The slope is positive when acceleration is positive, and negative when acceleration is negative.

V-T graph - Positive acceleration — Figure 7. Velocity-time graph with acceleration in the positive direction (eastward in this case).

V-T graph - Negative acceleration — Figure 8. Velocity-time graph with acceleration in the negative direction (westward in this case).