Definitions and postulates
Book traversal links for Definitions and postulates
Measuring angles
Classically, we consider a full rotation to be \(360^\circ\). This is when the terminal arm of an angle rotates until it comes back to the initial arm. Therefore, one degree is considered \(\frac{1}{360}\) of a full rotation.
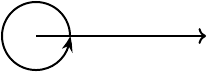
Classification of angles
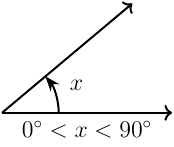
Acute
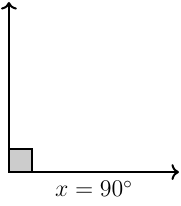
Right
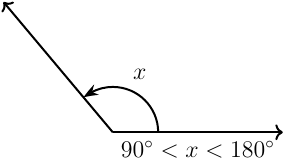
Obtuse
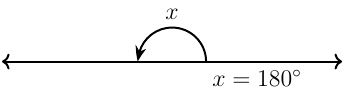
Straight
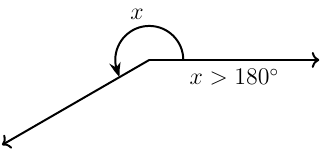
Reflex
Related angles
Two angles that share an arm (but are on two different sides of that arm) are called adjacent angles. Two angles that add up to \(90^\circ\) are called complementary angles. Two angles that add up to \(180^\circ\) are called supplementary angles.
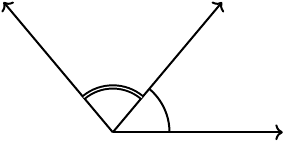
Adjacent angles
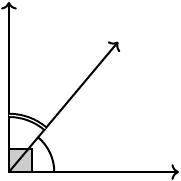
Complementary angles
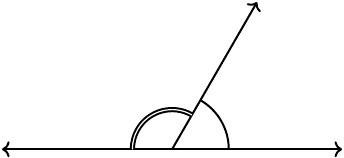
Supplementary angles
Intersecting lines
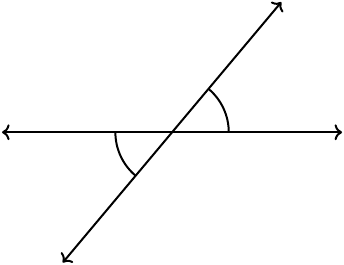
When two lines intersect, they create two pairs of opposite (also called vertically opposite), equal angles. Two lines that make an angle of \(90^\circ\) create four right angles; such lines are said to be perpendicular lines.
Parallel lines
Parallel lines in the same plane never intersect. If they are intersected by a third line, the resulting interior angles (see below) add up to \(180^\circ\). The shortest (perpendicular) distance between any two parallel lines is constant everywhere.
Transversal of parallel lines
A transversal is a a line that intersects two other (not necessary parallel) lines, creating 8 angles. The transversal of two parallel lines is interesting because the created angles are either congruent (equal) or supplementary. They are given particular names.
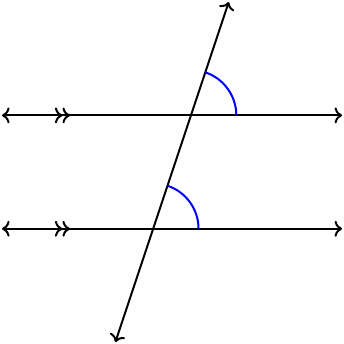
Corresponding angles (congruent)
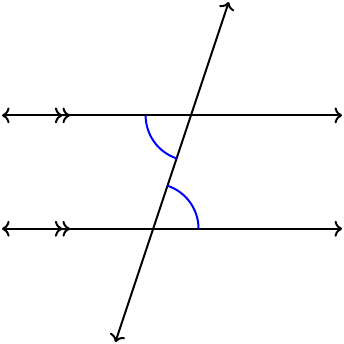
Alternate interior (congruent)
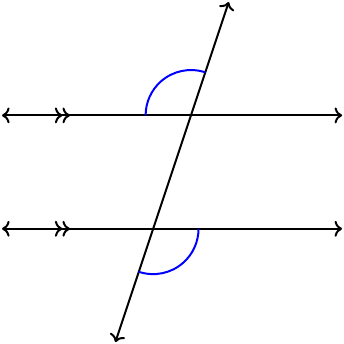
Alternate exterior (congruent)
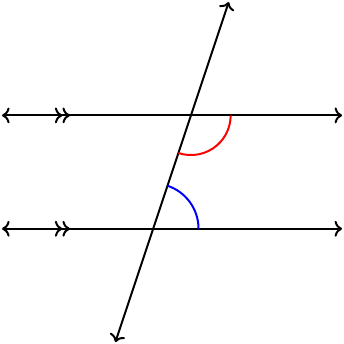
Consecutive interior (supplementary)
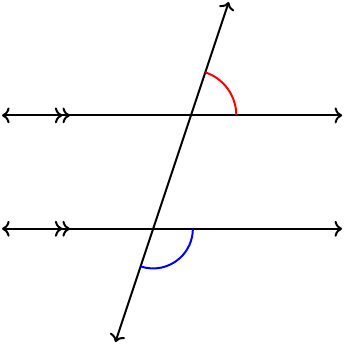
Consecutive exterior (supplementary)
Congruent and similar triangles
Similar triangles look like each other, but they are not necessarily copies of one another. Two triangles are similar if and only if
- their corresponding angles are congruent; or
- the ratios of their corresponding sides are equal.
Congruent triangles are exact copies of one another. Two triangles are congruent if and only if
- their corresponding sides are congruent;
- two pairs of corresponding angles are congruent and a pair of corresponding sides are congruent; or
- two pairs of corresponding sides are congruent and the angles enclosed by those sides are also congruent.