Basic concepts
Book traversal links for Basic concepts
Primitive geometric notions
(1) Point
A point is something that is defined only by its position. It has no width, length, depth, height or any dimension at all. In other words, it cannot be ‘measured’. We draw a point as a dot (which obviously has dimensions, but only because reality forces us to do so), and we typically give it an uppercase letter name like \(A,B,C,\cdots\).
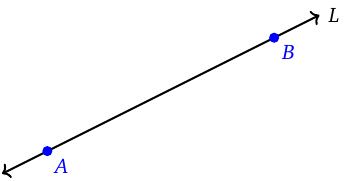
(2) Line
A line is a straight collection of points that extends infinitely in both directions. The notion of ‘straightness’ is taken intuitively. A line is drawn as a straight segment with arrowheads on both ends to indicate that it extends infinitely. A line contains an infinite number of points. It is named after any two (or more) points on it. For example, the line that has points \(A\) and \(B\) on it is denoted by \(\overleftrightarrow{AB}\) or \(\overleftrightarrow{BA}\). Note the double-headed arrow on top of \(AB\), which is the notation of a line. A line can also be given a single-letter name like \(L\), in which case we usually drop the double-headed arrow on top. A line does not have length, because it extends infinitely. However, it has a general direction. If we rotate a line, we change its direction.
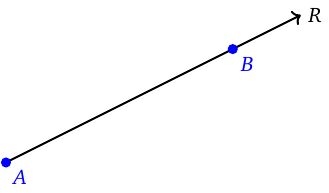
Ray
We can think of a ray as a ‘half-line’. A ray is a straight collection of points that extends infinitely in one direction only but ‘ends’ at a particular point on the other side. This point is called the end point of the ray. Like a line, a ray may be named by two points on it. A ray that has \(A\) as its end point and \(B\) as another point on it is denoted by \(\overrightarrow{AB}\). Note that there is a one-headed arrow on top, and that the end point must come first. A ray may also be given a single-letter name like \(R\), in which case we usually drop the single-headed arrow on top. A ray does not have length, because it extends infinitely. Like a line, a ray has a direction.
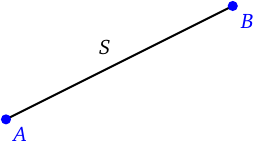
Segment
A segment is a finite part of a line. It begins and ends at a particular points. A segment is named after those two points. The segment that starts at \(A\) and ends at \(B\) is denoted by \(\overline{AB}\) or \(\overline{BA}\). Note the bar with no arrowheads on top. We may also give a segment a single-letter (usually lowercase) name like \(s\), in which case we usually drop the bar on top. Like a line, a segment has a direction, but unlike a line it has a length. A segment (a bit counter-intuitively) has an infinite number of points, too.
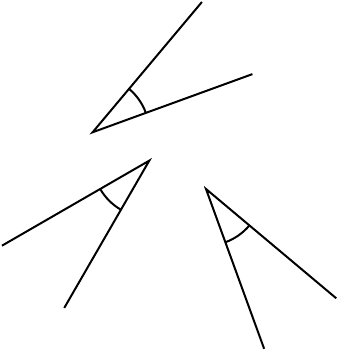
Angle
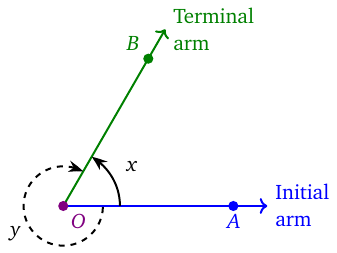
An angle is formed by two rays sharing their end points. The common end point is called the vertex of the angle, and the rays the arms of the angle. You may think of the angle as being formed by the two arms starting together at the same position, but one of them stays there and the other rotates around the vertex to form the angle. The arm that stays is called the initial arm, and the other the terminal arm. The angle is what the terminal arm sweeps as it moves. It is the change in the direction from the initial to the terminal arm.
(3) Plane
A plane is an infinite, flat collection of points. The notation of ‘flatness’ is taken intuitively. A plane extends infinitely in all of these ‘flat’ directions. A plane has not only an infinite number of points, but an infinite number of lines with different directions. A line in a plane divides the plane into two hemiplanes, and into three sets of points: one on each ‘side’ of the line and another on the line itself.
Primitive geometric relations
(1) Containment
- A point may or may not be contained in a line.

Point \(P\) is contained in the line
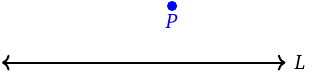
Point \(P\) is not contained in the line
- A point may or may not be contained in a plane.
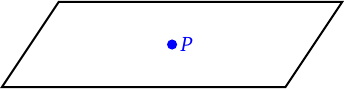
Point \(P\) is contained in the plane
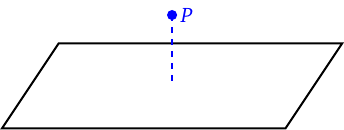
Point \(P\) is not contained in the plane
- a line may or may not be contained in a plane. If a line is contained in a plane, then every point of that line is also contained in the plane.

The line is contained in the plane
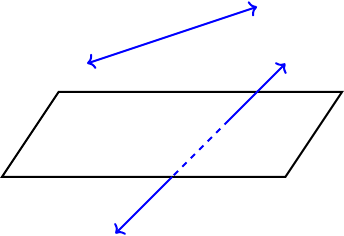
The line is not contained in the plane
(2) Betweenness
This is a relation between three points. If points \(A,B\) and \(C\) are such that \(B\) is between \(A\) and \(C\), then a ray from \(A\) to \(C\) will pass through \(B\) before reaching \(C\).
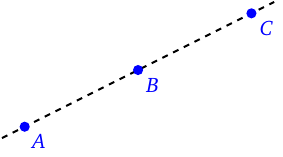
Point \(B\) is between \(A\) and \(C\)
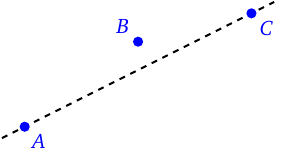
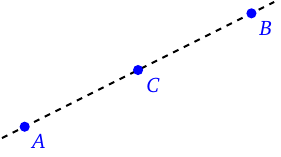
Point \(B\) is not between \(A\) and \(C\)
(3) Congruence
We can think of congruent geometric entities as those that can be ‘exactly overlaid’ on top of each other, so they have a one-to-one point correspondence. In other words, they are exact copies of one another.
- Two segments are congruent if and only if they have the same length, regardless of their orientation (direction).
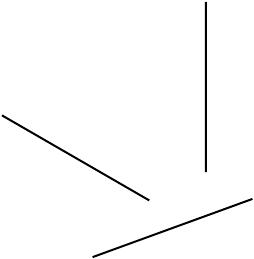
- Two angles are congruent if and only if they have the same measurement, regardless of their orientation.