Relative motion
كتاب روابط اجتياز لـ Relative motion
- Motion is always relative. This is because we must use a reference point to determine position, and motion will be relative to that reference point.
- When we speak of motion without specifying the reference point (or object), it is always implied; it is never entirely absent.
- The reference when we speak of motion near the surface of the Earth is the ground.
- We express the relative velocity of object \(A\) in relation to object \(B\) as \(\vec{v}_{AB}\).
- Relative velocities can be added as vectors using the ‘tip-to-tail’ or the ‘chain’ rule as follows \[\vec{v}_{\color{blue}{A}\color{green}{B}}=\vec{v}_{\color{blue}{A}\color{red}{C}}+\vec{v}_{\color{red}{C}\color{green}{B}}\]
- Remember that multiplying a vector by \(-1\) simply flips its direction, so \[\vec{v}_{AB}=\color{red}{-}\vec{v}_{BA}\]
- Using these principles, we solve problems of relative motion in the following steps
- Choose a unique letter to represent every object of interest in the problem.
- Determine the reference object for every velocity of interest. Write the symbol for that velocity with two letters as subscripts: the letter of the moving object, then the letter of the reference object. For example, if the moving object is a car, and the reference object is the ground, then you may write \(\vec{v}_{cg}\).
- Write your vector equation so that the velocity you are interested in is on the left side of the equation, and all other (available) velocity are on the right side, added together with the chain rule as described above.
- You may have one (or more) velocity in the reverse direction. For example, you may have the velocity of the train relative to the ground \(\vec{v}_{tg}\) but you want \(\vec{v}_{gt}\). Remember that \(\vec{v}_{gt}=-\vec{v}_{tg}\). Rewrite the equation to reflect the velocities that are given (or that can be calculated).
- You may want to draw a diagram to show how these vectors are added (tip-to-tail) to one another. This may help you determine the directions.
- Use your mathematical knowledge as appropriate to solve.
A boat is headed eastward straight across from a river bank to the other. The river flows at a rate of 2 m/s [South]. If the boat can maintain a water speed of 5 m/s, find the velocity of the boat relative to the ground.
We choose g for the ground, b for the boat, and w for the water. We are interested in \(\vec{v}_{bg}\), so we write our equation as follows
\[\vec{v}_{bg}=\vec{v}_{bw}+\vec{v}_{wg}\]The \(\vec{v}_{bw}\) is the water speed of the boat. We know from the question that it is headed eastward. The \(\vec{v}_{wg}\) is the velocity of the current relative to the ground. We know from the question that goes southward.
We draw a vector diagram to illustrate the relation between the vectors. This is the graphical representation of the equation that we wrote above. From this we can calculate the magnitude of \(\vec{v}_{bg}\) as
\[v_{bg}=\sqrt{v_{bw}^2+v_{wg}^2}=\sqrt{5^2+2^2}=\sqrt{29}\approx 5.4\text{ m/s}\]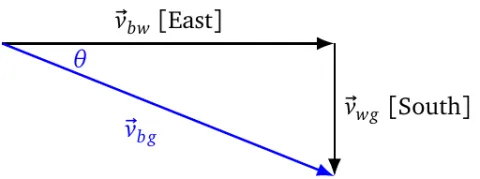
We can also calculate the direction of the velocity by finding \(\theta\) as
\[\theta=\tan^{-1}\frac{v_{wg}}{v_{bw}}=\tan^{-1}\frac{2}{5}\approx 22^\circ\]Therefore, the velocity of the boat relative to the ground is 5.4 m/s [E \(22^\circ\) S].