Characteristics of exponential functions

Domain

The domain of an exponential function is always all real numbers.

Range

The range of the parent exponential function $f(x)=b^x$ is $\{y\in\mathbb{R}\mid y\gt 0\}$. It is affected by vertical translation and reflection around the $x$-axis (see the table below).

$x$-intercept

The parent exponential function $f(x)=b^x$ never crosses the $x$-axis; hence it has no roots. It can have a single root if and only if it is vertically translated so that it crosses the $x$-axis.

$y$-intercept

The parent exponential function $f(x)=b^x$ always passes through the point $(0,1)$. It always has a $y$-intercept. The exact location of the $y$-intercept is affected by vertical stretch/compression and vertical translation.

Horizontal asymptote

An exponential function always has a horizontal asymptote. The parent function $f(x)=b^x$ has the asymptote at $y=0$ (i.e. the $x$-axis). The location of the asymptote is affected by vertical translation only.

End behaviour

	$\boldsymbol{0\lt b\lt 1}$	$\boldsymbol{b\gt 1}$
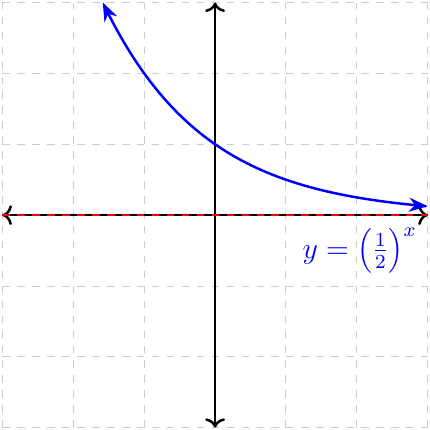
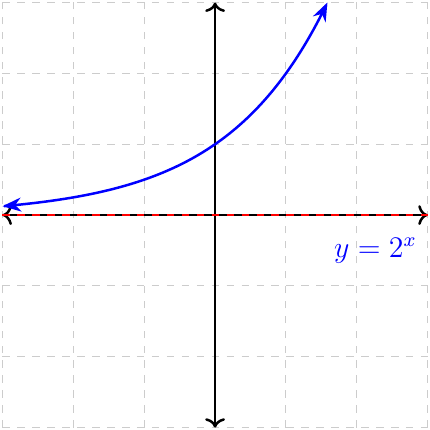
$\boldsymbol{f(x)=b^x}$	$Exponential function - base less than unit$ $y\to\infty$ as $x\to-\infty$ $y\to 0$ as $x\to\infty$ Decreasing Range $\{y\in\mathbb{R}\mid y\gt 0\}$	$Exponential function - base greater than unit$ $y\to 0$ as $x\to-\infty$ $y\to\infty$ as $x\to\infty$ Increasing Range $\{y\in\mathbb{R}\mid y\gt 0\}$
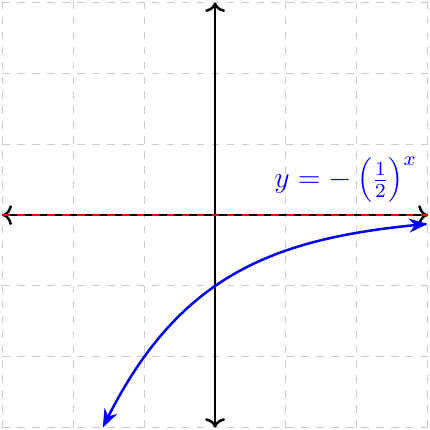
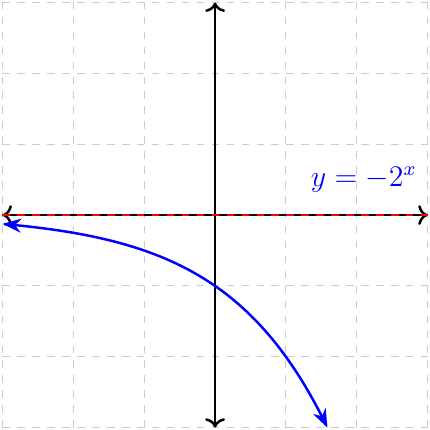
$\boldsymbol{f(x)=-b^x}$	$Exponential function - base less than unit - reflected$ $y\to-\infty$ as $x\to-\infty$ $y\to 0$ as $x\to\infty$ Increasing Range $\{y\in\mathbb{R}\mid y\lt 0\}$	$Exponential function - base greater than unit - reflected$ $y\to 0$ as $x\to-\infty$ $y\to-\infty$ as $x\to\infty$ Decreasing Range $\{y\in\mathbb{R}\mid y\lt 0\}$

In the table above, $0$ is the location of the asymptote, so this changes if the function is vertically translated.

Increasing and decreasing intervals

An exponential function is either always increasing or always decreasing. A function that is always increasing or always decreasing over its entire domain is called a monotone. Therefore, an exponential function is monotone increasing or monotone decreasing depending on the base, and whether or not it is reflected around the $x$-axis (see the table above).

	\(\boldsymbol{0\lt b\lt 1}\)	\(\boldsymbol{b\gt 1}\)
\(\boldsymbol{f(x)=b^x}\)	$Exponential function - base less than unit$ \(y\to\infty\) as \(x\to-\infty\) \(y\to 0\) as \(x\to\infty\) Decreasing Range \(\{y\in\mathbb{R}\mid y\gt 0\}\)	$Exponential function - base greater than unit$ \(y\to 0\) as \(x\to-\infty\) \(y\to\infty\) as \(x\to\infty\) Increasing Range \(\{y\in\mathbb{R}\mid y\gt 0\}\)
\(\boldsymbol{f(x)=-b^x}\)	$Exponential function - base less than unit - reflected$ \(y\to-\infty\) as \(x\to-\infty\) \(y\to 0\) as \(x\to\infty\) Increasing Range \(\{y\in\mathbb{R}\mid y\lt 0\}\)	$Exponential function - base greater than unit - reflected$ \(y\to 0\) as \(x\to-\infty\) \(y\to-\infty\) as \(x\to\infty\) Decreasing Range \(\{y\in\mathbb{R}\mid y\lt 0\}\)