Characteristics of polynomials
كتاب روابط اجتياز لـ Characteristics of polynomials
| Odd-degree | Even-degree | ||
|---|---|---|---|
| Domain | \(\{x\in\mathbb{R}\}\) | \(\{y\in\mathbb{R}\}\) | |
| Range | \(+\)ve leading coefficient | \(\{x\in\mathbb{R}\}\) | \(\{y\in\mathbb{R}\mid y\ge k\) where \(k\in\mathbb{R}\}\) \(k\) is the absolute minimum |
| \(-\)ve leading coefficient | \(\{y\in\mathbb{R}\mid y\le k\) where \(k\in\mathbb{R}\}\) \(k\) is the absolute maximum |
||
| End behaviour | \(+\)ve leading coefficient |
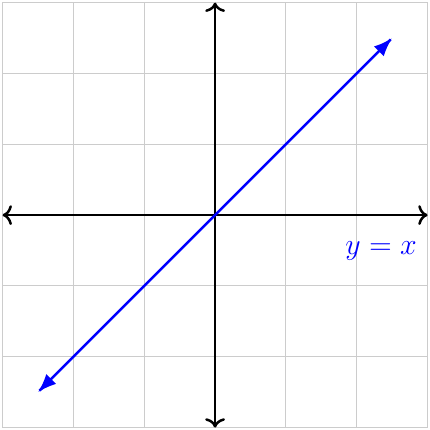
\(y\to-\infty\) as \(x\to-\infty\) \(y\to+\infty\) as \(x\to+\infty\) From QIII to QI |
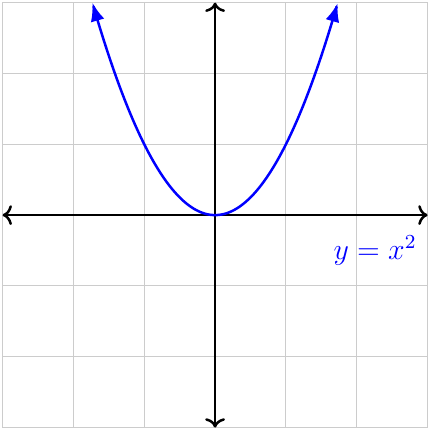
\(y\to+\infty\) as \(x\to-\infty\) \(y\to+\infty\) as \(x\to+\infty\) From QII to QI |
| \(-\)ve leading coefficient |
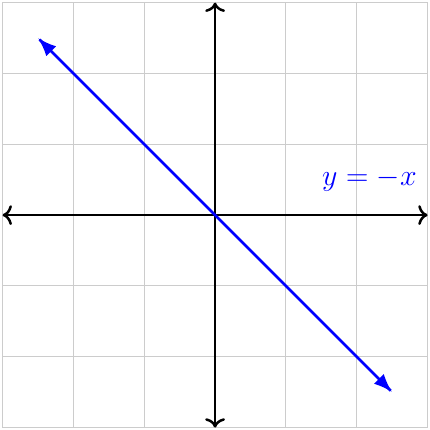
\(y\to+\infty\) as \(x\to-\infty\) \(y\to-\infty\) as \(x\to+\infty\) From QII to QIV |
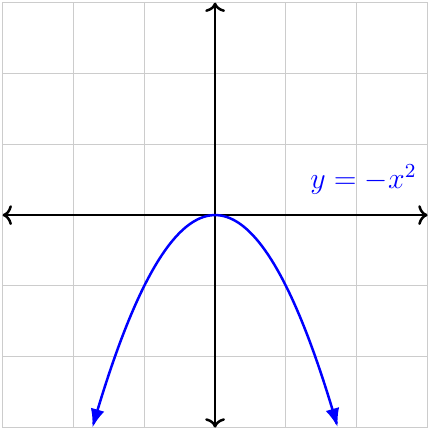
\(y\to-\infty\) as \(x\to-\infty\) \(y\to-\infty\) as \(x\to+\infty\) From QIII to QIV |
|
| Symmetry | May be odd (but not always) Never even |
May be even (but not always) Never odd |
Number of real roots* | Minimum | \(1\) | \(0\) |
| Maximum | \(n\) | \(n\) | |
| Number of turning points* | Minimum | \(0\) (always even) | \(1\) (always odd) |
| Maximum | \(n-1\) | \(n-1\) | |
*\(n\) is the degree of the polynomial.