Sinusoidal functions

Definitions and characteristics

Sinusoidal functions are ‘sine-like’ functions. At this level, we only study sine and cosine functions, but combinations of them are also sinusoidal functions. Sinusoidal functions are periodic, which means they repeat the exact behaviour every fixed interval, called the period of the function. Because of this, they have a minimum and a maximum, and the function value is always bounded between them.

The phase of a point on the graph of the function is the position of that point within the period.

They have the following four characteristics.

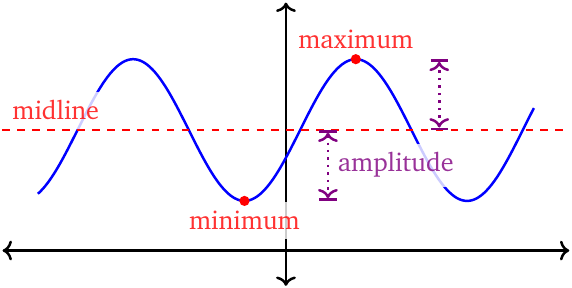
  • Midline (axis). This is the horizontal line located midway between the minimum and the maximum. It is also the vertical compared to the parent function. \[\text{midline}: y=\dfrac{\text{max}+\text{min}}{2}\]
  • Amplitude. This is always a positive number. It is the distance between the midline and either the minimum or the maximum. \[\text{amplitude}=\dfrac{\text{max}-\text{min}}{2}\]
    Sinusoidal function minimum, maximum, midline and amplitude
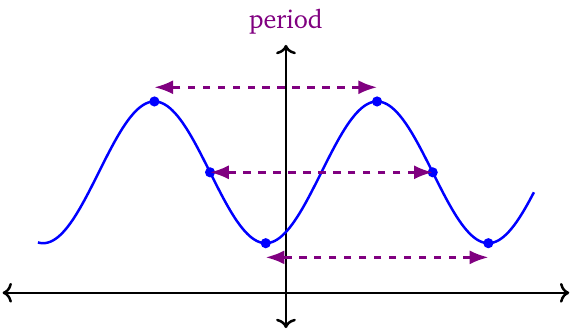
  • Period. This is the shortest interval after which the function starts repeating the same behaviour. It is also the shortest distance between two points of the same phase. The easiest way to measure the period is to measure the distance between two maxima or two minima.
    sinusoidal function period
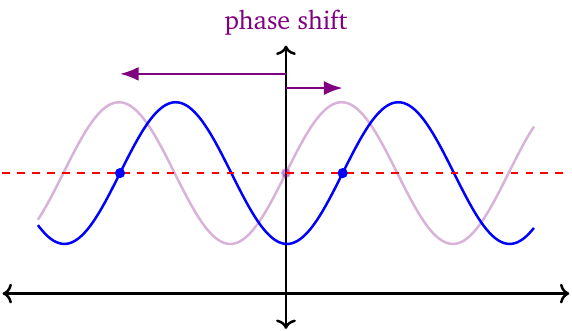
  • Phase shift. This is the horizontal shift compared to the parent function. The sine function starts (at the \(y\)-axis) at its midline, while the cosine starts at the maximum. Therefore, we measure the phase shift according to whether we want to express the function as a sine or a cosine.
    sinusoidal function phase shift (sine)
    sinusoidal function phase shift (cosine)

Transformations

\begin{align} y &= a\sin[k(x-d)]+c \\ y &= a\cos[k(x-d)]+c \end{align}

The characteristics are related to the transformations as follows.

  • Amplitude \(=\lvert a\rvert\) (vertical stretch or compression by a factor of \(\lvert a\rvert\))
  • Midline. \(y=c\) (vertical translation by \(c\))
  • Period \(=\dfrac{360^\circ}{\lvert k\rvert}\) (horizontal stretch or compression by a factor of \(\frac{1}{\lvert k\rvert}\))
  • Phase shift \(=d\) (horizontal translation by \(d\))

The function is reflected around the \(x\)-axis if and only if \(a\lt 0\), and around the \(y\)-axis if and only if \(k\lt 0\).