Mathematics (MTH1W)

Important terminology

• All operations. Addition, subtraction, multiplication and division are called arithmetic operations. Each of these takes in two numbers (called the operands), and produces some value(s) (called the result). The sign that indicates the type of operation is called the operator. Therefore,
  • the addition operator is \(+\);
  • the subtraction operator is \(-\);
  • the multiplication operator is \(\times\);
  • the division operator is \(\div\);
  The operator is always written between the operands, followed by an equal sign \(=\), then the result. The equal sign is pronounced as ‘equal’, as ‘is’, as ‘results in’, as ’gives’.
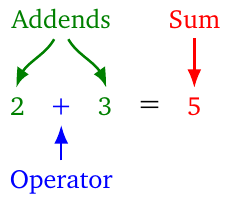
• Addition. Take for example the expression \(2+3=5\),
  • The two numbers \(2\) and \(3\) that are added are called the addends.
  • The result \(5\) of addition is called the sum.
  • The operation is pronounced as ‘2 plus 3’, as ‘2 and 3’, or as ‘3 more than 2’.
  The words ‘total’ and ‘and’ imply addition. It may also be implied by words like ‘increase’.



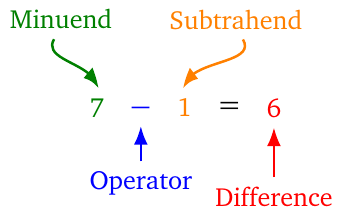
• Subtraction. Take for example the expression \(7-1=6\),
  • The first number \(7\) in subtraction is called the minuend.
  • The second number \(1\) in subtraction is called the subtrahend.
  • The result of subtraction is called the difference.
  • The operation is pronounced as ‘7 minus 1’, as ‘one less than 7’, as ‘7 less 1’, or as ‘7 take away 1’
  • We say that we \(1\) is subtracted from \(7\), not the other way around. We may say that \(7\) is reduced by \(1\). We do not say that \(7\) is subtracted by \(1\).
  The word ‘change’ implies subtraction. It may also be implied by words like ‘reduce’ or ‘decrease’.



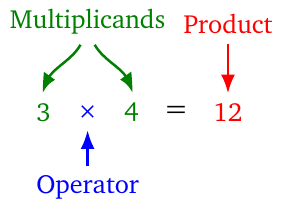
• Multiplication. Take for example the expression \(3\times 4=12\).
• The two numbers \(3\) and \(4\) that are multiplied are called the multiplicands.
• The result of multiplication is called the product.
• The operation is pronounced as ‘3 times 3’, or as ‘3 by 4’
• We say that we have four threes (i.e., that three is counted four times), or three fours (i.e., that four is counted three times); or that \(3\) is increased by a factor of \(4\), or \(4\) is increased by a factor of \(3\).



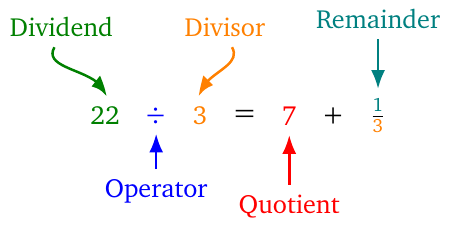
• Division. Take for example the expression \(22\div 3=7+\frac{1}{3}\),
  • The first number \(22\) in division is called the dividend.
  • The second number \(3\) in division is called the divisor.
  • There are two possible results of division. The whole part, \(7\) in this example, is called the quotient. The numerator, \(1\) in this example, of the fractional part is called the remainder.
  • The operation is pronounced as ‘22 divided by 3’; or ‘22 over 3’.
  • We say that ‘\(22\) divided by \(3\) is \(7\) with a remainder of \(1\)’; or that ‘\(3\) goes into \(22\) seven times with a remainder of \(1\)’
  The word ‘quotient’, ‘ratio’ or ‘rate’ implies division. Ratio is expressed as one number over another as in \(\frac{22}{3}\). In this notation, the number above is called the numerator, the one below is called the denominator, and the line between then is called the fraction bar.

Factors, divisors and multiples

• The word ‘factor’ as a nouns means ‘multiplier’.
• The word ‘factor’ as a verb means ‘to express as a product’.
• If the remainder of \(a\div b\) is zero, we say that ‘\(\boldsymbol{b}\) is a divisor of \(\boldsymbol{a}\)’, or that ‘\(\boldsymbol{b}\) is a factor of \(\boldsymbol{a}\)’. There is no contradiction, because the statement \(a\div b=c\) is equivalent to the statement \(a=b\times c\). Multiplication and division are two faces of the same coin.
• For the same reason, if the remainder of \(a\div b\) is zero, we say that ‘\(\boldsymbol{a}\) is a multiple of \(\boldsymbol{b}\).
• The terms ‘factor’, ‘divisor’, and ‘multiple’ are almost always used with whole numbers. This means that, if we restrict ourselves to positive whole numbers only
• a factor or a divisor of a number is always less than or equal to that number; and
• a multiple of a number is always greater than or equal to that number.