Kinematics

Vector versus scalar quantities

Vector Scalar
Position: A fundamental, intuitive quantity.
Usually denoted by \(\vec{d}\) or \(\vec{s}\).
Displacement: Change of position.
Usually denoted by \(\Delta\vec{d}\) or \(\Delta\vec{s}\).
\(\Delta\vec{d}=\vec{d}_{\text{final}}-\vec{d}_{\text{initial}}\)		 Distance: Path length.
Usually denoted by \(\Delta d\).
Velocity: Rate of change of position (or displacement).
Usually denoted by \(\vec{v}\).
\(\vec{v}=\dfrac{\Delta\vec{d}}{\Delta t}\)		 Speed: Rate of change of distance.
Usually denoted by \(v\).
\(v=\dfrac{\Delta d}{\Delta t}\)
Acceleration: Rate of change of velocity.
Usually denoted by \(\vec{a}\)
\(\vec{a}=\dfrac{\Delta\vec{v}}{\Delta t}\)
Important Note

Displacement depends only on the initial and final points. Distance depends on how an objects goes from the initial to the final points.

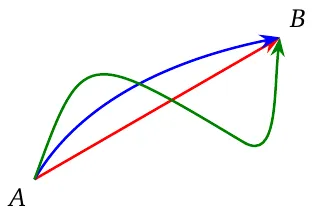
Displacement versus distance
The red arrow represents the displacement. It only depends on \(A\) and \(B\). If an object does not go in a straight line from \(A\) to \(B\), the length of the path is greater than the magnitude of the displacement, and it depends on how the object moves from \(A\) to \(B\) (the blue and the green lines).

For the same object in the same motion,

  • distance \(\ge\) magnitude of displacement
  • speed \(\ge\) magnitude of velocity

Total displacement

The total displacement is either

  • the sum of the individual displacements; or
  • the difference between the very initial position and the very final position.

Average versus instantaneous velocity and acceleration

The average velocity (\(\vec{v}_{\text{av}}\)) between two points is the ratio of the displacement to the time taken for this to happen.

\[\vec{v}_{\text{av}}=\dfrac{\Delta\vec{d}}{\Delta t}\]

The instantaneous velocity (\(\vec{v}_{\text{inst}}\) or simply \(\vec{v}\)) at one point is the velocity at that point exactly. It is impossible to determine with the conventional methods (calculus is required). However, it can be estimated as the average velocity over a very small time interval.

Similarly, the average acceleration (\(\vec{a}_{\text{av}}\)) between two points is the ratio of the change of velocity to the time taken for this to happen.

\[\vec{a}_{\text{av}}=\dfrac{\Delta\vec{v}}{\Delta t}\]

The instantaneous acceleration (\(\vec{a}_{\text{inst}}\) or simply \(\vec{a}\)) at one point is the acceleration at that point exactly. It is impossible to determine with the conventional methods (calculus is required). However, it can be estimated as the average acceleration over a very small time interval.

Kinematics graphs

  • Read directly from the graph only that which is represented on the vertical axis (i.e., what we often refer to as the \(y\)-value).
    • from the displacement-time graph we read displacement on the vertical axis;
    • from the velocity-time graph we read velocity on the vertical axis;
    • from the acceleration-time graph we read acceleration on the vertical axis;
  • The average rate of change between two points is the slope of the secant line (the line that connects those two points). It is interpreted in the context of the graph.
    • The slope of the secant line in the displacement-time graph is the average velocity.
    • The slope of the secant line in the velocity-time graph is the average acceleration.
  • The instantaneous rate of change at one given point is the slope of the tangent line (the line that ‘touches’ the graph at that point). It is interpreted in the context of the graph.
    • The slope of the tangent line in the displacement-time graph is the instantaneous velocity.
    • The slope of the tangent line in the velocity-time graph is the instantaneous acceleration.
  • The area under the curve (AUC) is the net change in the product of the vertical axis and the horizontal axis. Areas above the horizontal axis are considered a positive change. Areas below the horizontal axis are considered a negative change. AUC is interpreted in the context of the graph.
    • The AUC between two points in the velocity-time graph is the net displacement between those two points.
    • The AUC between two points in the acceleration-time graph is the net change in velocity between those two points.

BEWARE: sign denotes direction when dealing with vectors in one dimension. It is a common mistake to think of positive values as being ‘larger’ than negative values. In this context, negative only means they go in the direction taken to be negative.

Important Note

When dealing with vectors in one dimension, SIGN DENOTES DIRECTION. It does not mean smaller or larger, and does not mean increasing or decreasing.

The AUC is considered