Graphs of polynomials

A polynomial crosses the \(x\)-axis at its roots. It may have more than one root at a given point. This is called the order of the root.

• At odd-order roots, the graph of a polynomial crosses the \(x\)-axis. As the order increases, the graph becomes flatter around the \(x\)-axis. For orders 3 or more, the graph will also have a point of inflection (where the curvature changes from concave up to down or vice versa) at the root.
• At even-order roots, the graph of a polynomial will bounce off the \(x\)-axis. As the order increases, the graph becomes flatter around the \(x\)-axis. The graph will have a turning point at even-order roots.

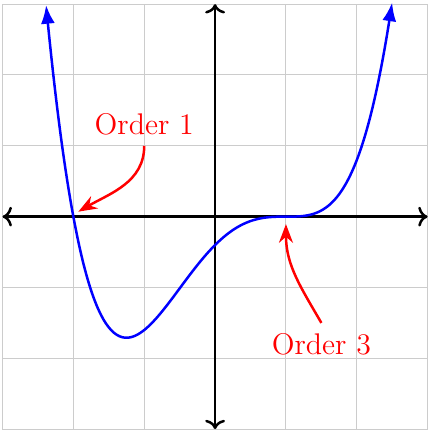
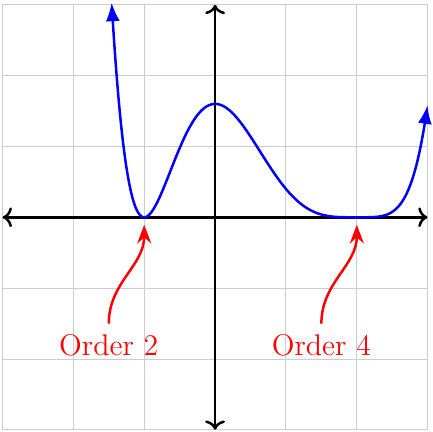
When graphing polynomials, we also have to consider their end behaviour. Refer to Characteristics of polynomials.