Vectors

Definition

• A vector is a quantity that is fully defined by both its magnitude (how large or small it is) and its direction.
• A scalar is a quantity that is defined by its magnitude only is a scalar.
• The magnitude of a measured quantity is never negative.
• A vector inherently has direction. Vectors cannot be made into scalars, neither can scalars be made into vectors.
• Direction is always measured relative to a reference direction. A ‘reference’ is considered the ‘zero’ from which we start measuring.
• At high-school level, we typically deal with ‘free vectors’; i.e., vectors are not attached to a particular point. As long as we keep the direction and the magnitude unchanged, the vector remains constant, regardless of where it starts and where it ends.
• The zero vector \(\vec{0}\) is a vector with zero magnitude and an undefined direction. It is the only vector with zero magnitude.

Graphical representation

A vector is represented graphically by a linear segment with an arrowhead on one side.

• The length of the segment is proportional to the magnitude of the vector.
• The arrowhead indicates the direction.
• The end of the segment without the arrowhead is called the initial point or the tail of the vector
• The end with the arrowhead is called its terminal point or tip.

Notation

A vector is denoted by any of the following

• A single-letter name with an arrow on top, as in \(\vec{v}\).
• A single-letter name that is written in boldface and not italicized, as in \(\mathrm{\boldsymbol{v}}\).
• Its initial and terminal points (in this order) with an arrow on top, as in \(\vec{AB}\) which is the vector starting at \(A\) and ending at \(B\).

The magnitude of vector \(\vec{v}\) may be denoted simply by \(v\) or by \(\lVert\vec{v}\rVert\).

Denoting direction

The bearing is the reading of a compass. It is usually represented in two common ways.

• Quadrant bearing.
• The reference direction is typically north or south, and measurement is done towards the east or the west. The notation [N\(20^\circ\)E] means “from the north, we measure \(20^\circ\) towards the east”.
• Some also accept using east or west as the reference and measuring towards the north or the south.
• When going exactly in one of the cardinal directions, we just specify that one; e.g., [E] means “straight east”.
• The angle \(\theta\) in this notation is always such that \(0^\circ\lt\theta\lt 90^\circ\)
• A notation similar to quadrant bearing may be used in other contexts where there is no compass; e.g., [Forward \(50^\circ\) Right] means “starting from the forward direction we measure \(50^\circ\) towards the right”.
• Absolute bearing.
• The reference direction is always north.
• The angle is measured in a clockwise direction.
• The angle \(\theta\) is within one full rotation, so \(0^\circ\le\theta\lt 360^\circ\).
• The angle is typically written as a 3-digit number; e.g., \(075^\circ\).
• North is \(0^\circ\), east is \(90^\circ\), south is \(180^\circ\) and west is \(270^\circ\).

The angle of elevation is the angle relative to the horizontal plane measured upwards. The angle of depression is the angle relative to the horizontal plane measured downward.

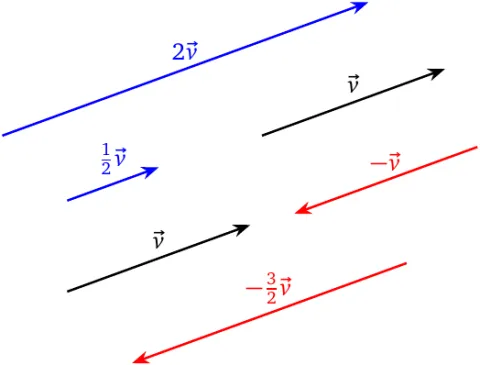
Multiplying a vector by a scalar

The result of multiplying a vector by a scalar is always a vector. The product \(k\vec{v}\), where \(k\) is a scalar and \(\vec{v}\) is a vector is

• the zero vector \(\vec{0}\) if and only if either \(k=0\) or \(\vec{v}=\vec{0}\);
• has the same direction as \(\vec{v}\) if and only if \(k\gt 0\); or
• has the exact opposite direction to that of \(\vec{v}\) if and only if \(k\lt 0\).

The previous definition means that \(k\vec{v}\) is parallel to \(\vec{v}\) if and only if neither of them is the zero vector.

The magnitude of \(k\vec{v}\) is equal to the product of the absolute value of \(k\) and the magnitude of \(\vec{v}\); i.e., \(\lVert k\vec{v}\rVert=\lvert k\rvert\,\lVert\vec{v}\rVert\). This implies that the magnitude of \(\vec{v}\) changes if and only if \(k\neq \pm1\).

Adding vectors

The fundamental rule of adding vectors is the tip-to-tail rule. We place the tip of one vector at the tail of the next, so that one vector ends where the next starts. The vector sum or the resultant is the vector that goes from the very first tail to the very last tip.

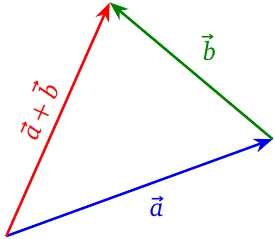
• The tip-to-tail rule is the one and only rule for vector addition. Every other rule you may hear of depends on it.
• We can only add vector quantities that are similar to one another; i.e. we cannot add displacement to velocity, or force to acceleration.
• We can only add vector quantities that are measured in the same unit of measurement.

In one dimension

Vectors are said to be in ‘one dimension’ if and only if they are parallel to one another. Vector addition in one dimension is simplified by the following.

1. Choose one of the two opposite directions to be positive; the other becomes automatically negative.
2. Replace the direction with the appropriate sign. For example, if you chose east to be positive, 20 m [E] becomes \(+20\) and 30 m [W] becomes \(-30\).
3. Add the signed numbers that you now have.
4. Interpret the result.
• The sign of the result indicates its direction (according to your choice).
• The absolute value of the result indicates the magnitude.

The tip-to-tail rule is still followed in one dimension, as shown in the next example.

Example: adding vectors in one dimension

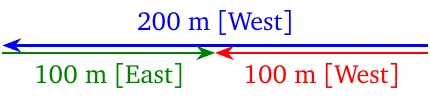
To add displacement of \(200\) m [West] to another of \(100\) m [East], we may choose \(+\) for West and \(-\) for East. The displacements then become \(+200\) and \(-100\). The resultant is \(+200-100=+100\). Since the resultant is positive, it goes West. Therefore, the resultant is \(100\) m [West].

In two dimensions

We draw vectors in a tip-to-tail manner as indicated above. The resultant of any two vectors makes a triangle with them. We solve the triangle to find the resultant. The method of solving the triangle depends on whether it is a right triangle (the vectors are perpendicular to each other) or not.

Perpendicular vectors

1. Pythagorean theorem. We calculate the magnitude of the resultant. The resultant is the hypotenuse of the right triangle. The vectors are its legs.
2. Inverse tangent. One of the given vectors is the opposite of an acute angle in the triangle, and the other is its adjacent. Choose carefully because this affects your interpretation.
3. Interpretation. Interpret the angle as the proper direction of the resultant.

Example: adding perpendicular vectors

To add 200 m [E] and 100 m [N], we draw them tip-to-tail to visualize the resultant, which is the red vector in the right triangle below. We can calculate the magnitude by the Pythagorean theorem as

\begin{align} d &= \sqrt{200^2+100^2} \\ &= \sqrt{50000}\approx 223.6 \mathrm{m} \end{align}

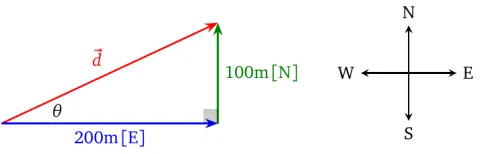
The angle \(\theta\) below has an opposite side of 100 m and an adjacent of 200 m. Therefore,

\begin{align} \tan \theta &= \dfrac{100}{200}=0.5 \\ \theta &= \tan 0.5 \approx26.6^\circ \end{align}

Therefore, the resultant is 224 m [E\(27^\circ\)N], which would be typically expressed as 224 m [N\(63^\circ\)E].

Non-perpendicular vectors

1. The law of cosines. We can always calculate the angle between the two vectors. We then have two sides in the triangle and an angle between them. We use the law of cosines to calculate the third side, which is the magnitude of the resultant.
2. The law of sines. We now know the three sides and one angle in the triangle. We use the law of sines to calculate the angle between the resultant and one of the vectors.
3. Interpretation. We finally have to interpret the angle as the proper direction of the resultant.

Example: adding two non-perpendicular vectors in two dimensions by solving triangles

To add 200 m [E\(20^\circ\)N] and 150 m [N\(60^\circ\)W], we draw them tip-to-tail to visualize the resultant, which is the red vector below. The three vectors make a triangle.

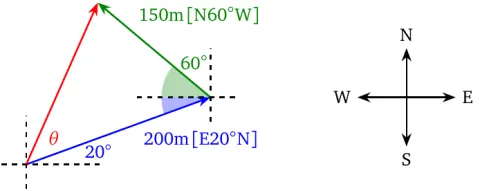
The angle between the two vectors is composed of two parts (shaded in the drawing); the blue is \(20^\circ\) (alternate angle) and the green is \(30^\circ\) (complementary). Therefore, the angle between the blue and green vectors is \(50^\circ\). Now we can use the law of cosines. Let the magnitude of the resultant be \(c\), then

\begin{align} c^2 &= a^2+b^2-2ab\cos C \\ &= 200^2+150^2-2(200)(150)\cos 50^\circ \\ &= 23932.74 \\ \therefore c &= 154.7 \mathrm{m} \end{align}

Now we calculate the angle \(\theta\) that the resultant makes with the blue vector using the law of sines.

\begin{align} \dfrac{\sin\theta}{150} &= \dfrac{\sin 50^\circ}{154.7} \\ \sin\theta &= 0.742771 \\ \theta &= \sin^{-1}0.742771 \approx 48^\circ \end{align}

To interpret the result, we have to state the direction relative to one of the cardinal directions. We note that the angle between the resultant and the east is \(\theta+20^\circ=68^\circ\), which means the angle between the resultant and the north is \(90^\circ-68^\circ=22^\circ\).

Therefore, the resultant is 155 m [N\(22^\circ\)E].

Notice how vector addition in two dimensions is a lot more complicated than it is in one dimension. In three dimensions (which is the reality we live in), it becomes even more complicated. Furthermore, the previous method works when we are adding two vectors. If we want to add more than two vectors, we have to do them pairwise (two at a time). We will end up solving \(n-1\) triangles to add \(n\) vectors.

An easier way to add vectors is to use vector decomposition, which has more benefits than just simplifying the calculations.

Vector decomposition

Vector decomposition means to express a vector as the sum of two (or more) other vectors, called in this context the components of the vector. For reasons beyond this scope, we use perpendicular dimensions for those components.

• The choice of the exact dimensions is arbitrary, as long as they are perpendicular.
• Once the perpendicular dimensions are chosen, we have a unique decomposition of any given vector in those dimensions.
• The components go from the initial point of the vector, in a tip-to-tail manner, along the chosen dimensions, ending at the terminal point of the vector.
• Perpendicular dimensions are independent. We can deal with each of them as if the other(s) did not exist.
• Scalar quantities are the same in all dimensions, since scalars do not have a direction.
• Time, being a scalar, is typically an important link between different dimensions.

The magnitude of the components in two dimensions is obtained easily by noting that they make a right triangle, in which the vector is the hypotenuse.

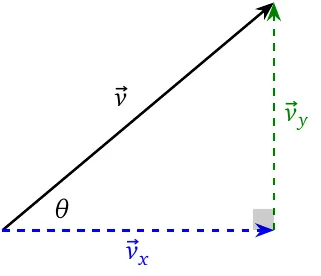
The perpendicular dimensions and typically (but do not need to be) horizontal and vertical, and are typically (but do not need to be) called the \(x\)- and the \(y\)-components. Their magnitude is calculated as \[v_x=v\cos\theta\] \[v_y=v\sin\theta\]

• The opposite to the angle (not necessarily the vertical component) takes the sine ratio.
• The adjacent to the angle (not necessarily the horizontal component) takes the cosine ratio.

Adding vectors by decomposition

• Choose your perpendicular dimensions. This is usually quite evident from the context of the problem.
• Choose which direction in each dimension will be positive. We call this the ‘sign convention’. Indicate your sign convention on your sketches or equations.
• Find the angles between your vectors and the perpendicular dimensions.
• Decompose your vectors in those perpendicular dimensions.
• Assign \(+\) or \(-\) as appropriate to your components according to your sign convention.
• Add all components in the same dimension together. You will get one component of the result per dimension.
• Add the components of the result (from the previous step) to find the final vector sum.
• Interpret your findings appropriately.

Example: vector addition by decomposition

To add the vectors 100 m [E\(25^\circ\)N], 150 m [N\(50^\circ\)W], and 120 m [S\(20^\circ\)E], we first sketch them, indicating the directions and the sign convention on the sketch. We then decompose them into the perpendicular east-west (E-W) and north-south (N-S) dimensions. We choose east and north to be the positive directions. Decomposition yields the following.

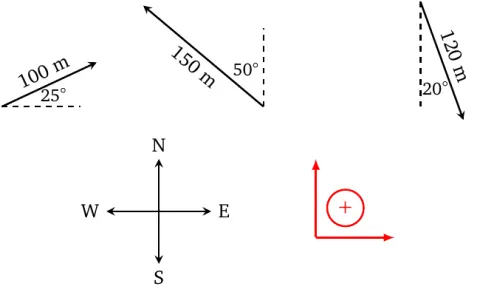
	E-W	N-S
100 m [E\(25^\circ\)N]	\(\color{blue}{+}100\cos 25^\circ\approx\color{blue}{+{}}90.6308\)	\(\color{blue}{+}100\sin 25^\circ\approx\color{blue}{+{}}42.2618\)
150 m [N\(50^\circ\)W]	\(\color{red}{-}150\sin 50^\circ\approx\color{red}{-{}}114.9067\)	\(\color{blue}{+}150\cos 50^\circ\approx\color{blue}{+{}}96.4181\)
120 m [S\(20^\circ\)E]	\(\color{blue}{+}120\sin 20^\circ\approx\color{blue}{+{}}41.0424\)	\(\color{red}{-}120\cos 20^\circ\approx\color{red}{-{}}112.7631\)
Sum	\(\color{blue}{+{}}16.7665\)	\(\color{blue}{+{}}25.9168\)

Both sums are positive, which means the E-W component goes in the east direction, and the N-S component goes in the north direction. We sketch the two components in a tip-to-tail manner to get their sum.

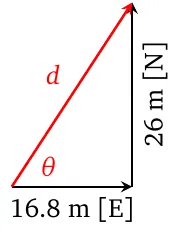
\(d=\sqrt{16.7665^2+25.9168^2}\approx 30.8673\)

\(\theta=\tan^{-1}\dfrac{25.9168}{16.7665}\approx 57^\circ\)

We interpret the result as a total displacement of 31 m [E\(57^\circ\)N], which is typically expressed as 31 m [N\(33^\circ\)E].