Applications near the surface of the Earth

Mass versus weight

Mass \(m\) is a measure of the amount of substance in an object. The mass of an object does not change depending on its position. For example, an object's mass near the surface of the Earth is the same as its mass in the outer space.
Weight \(W\) is the force of gravity \(F_g\) acting on an object. This depends on the mass of the object, but also on the strength of the gravitational field in which it is placed. An object in the outer space would have practically no weight if it is far enough from any major celestial body.
Near the surface of the Earth, the weight of an object is calculated as \[F_g=mg\] where \(g\) is the acceleration of gravity near the surface of the Earth, taken to be about 9.8 m/s² [downward].
Apparent weight or perceived weight is the normal force acting on an object. This depends on the totality of the forces acting on the object. For example, if you are in an elevator accelerating downward, you may feel ‘lighter’. It is not because your actual weight suddenly becomes smaller, but rather that the normal force acting on you becomes smaller.

Terminal speed

When an object moves through air (or any fluid) it encounters some resistance called the drag force, always acting opposite to the direction of motion. It is similar to friction when two solids move against each other. Drag force is much more complicated than the force of friction, but you only need to know the following about it

It is directly proportional to the square of the speed of the object.
It is directly proportional to the cross sectional area of the object perpendicular to the direction of motion; i.e. the area that faces the fluid while the object moves in it.
It is directly proportional to the density of the fluid.
It also depends on the surface characteristics of the object.

When an object is in free fall for a relatively significant time, it speeds up enough to make the drag force significant; then the object will not be in ‘free’ fall anymore. The faster the object moves, the larger the drag force, until it almost equals the force of gravity, at which point the net force on the object is zero and it neither speeds up nor slows down. This speed is called the terminal speed. It depends on many factors as described above.

Using this knowledge, we can understand how parachutes work to slow down the descent of a falling object.

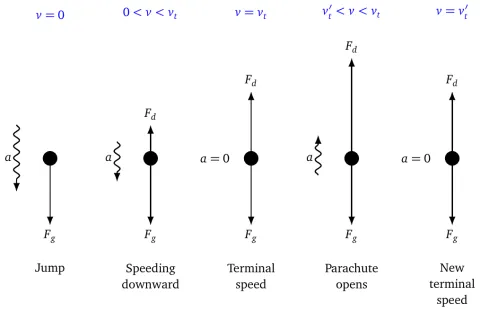
When the skydiver jumps off the plane, they are only under the effect of gravity, so they start to accelerate downwards at the rate of gravitational acceleration (9.8 m/s² [downward]).
As they gain speed, the drag force increases dramatically, the net downward force decreases, and the acceleration decreases. The acceleration is still downwards, and the skydiver is still speeding downwards, but at a slower rate.
Eventually, the drag force becomes almost equal to the force of gravity, and the skydiver is not accelerating anymore. The speed remains constant. This is the terminal speed \(v_t\).
When the parachute is opened, the surface area suddenly increases, thus increasing the drag force suddenly and dramatically. The net force, as well as the acceleration, are now acting upwards. The skydiver is still moving downwards, which means they are now slowing down.
As they slow down, the drag force gets smaller, until it balances the force of gravity again. However, during that time, the skydiver has slowed down to a new terminal speed \(v'_t\) based on the new conditions with the open parachute.