Right bisectors and circumcentre
Book traversal links for Right bisectors and circumcentre
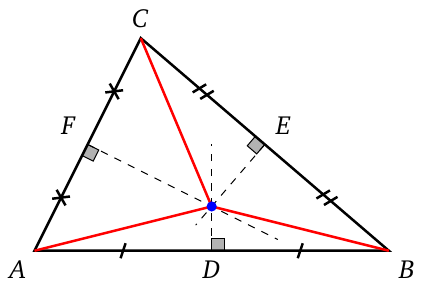
A right bisector of a triangle is a line that passes through the midpoint of a side and is perpendicular to that side. All three right bisectors of a triangle intersect at one and the same point, called the circumcentre of the triangle. The circumcentre is the centre of the circumscribed circle, which is the circle that passes through all vertices of the triangle.
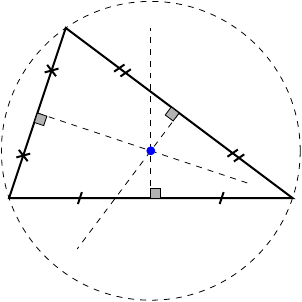
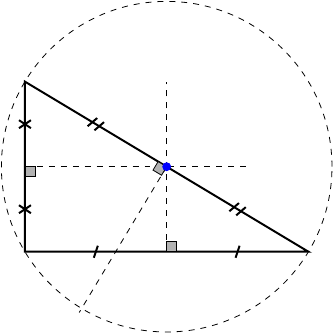
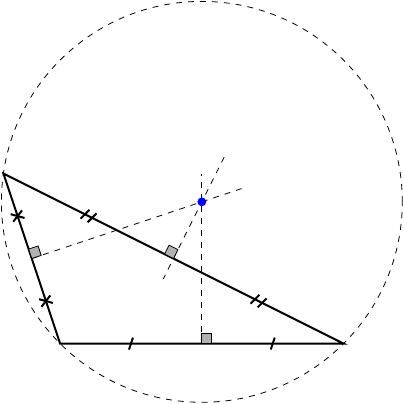
Theorems of right bisectors and circumcentre
- The circumcentre, being the centre of the circumscribed circle, is at the same distance from all vertices of a triangle.
- The circumcentre is inside an acute triangle, at the midpoint of the hypotenuse of a right triangle, and outside an obtuse triangle.