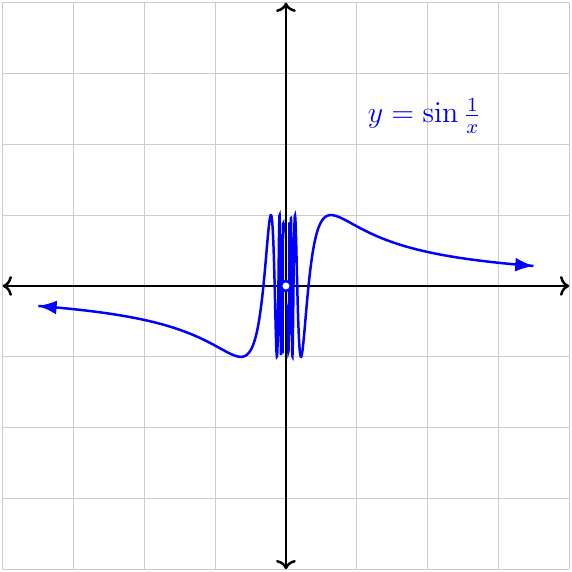
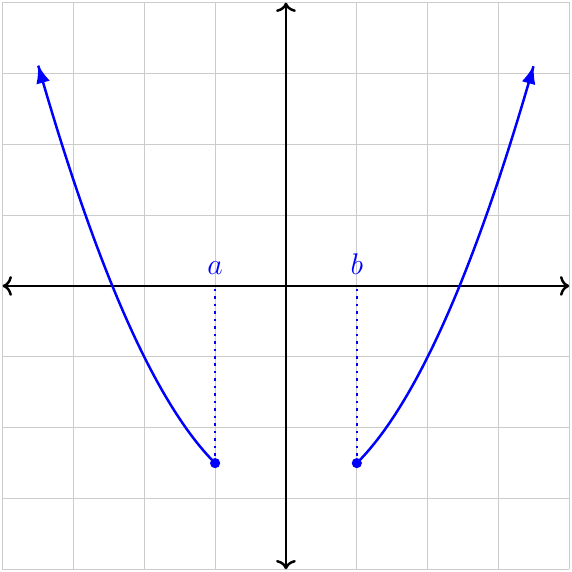
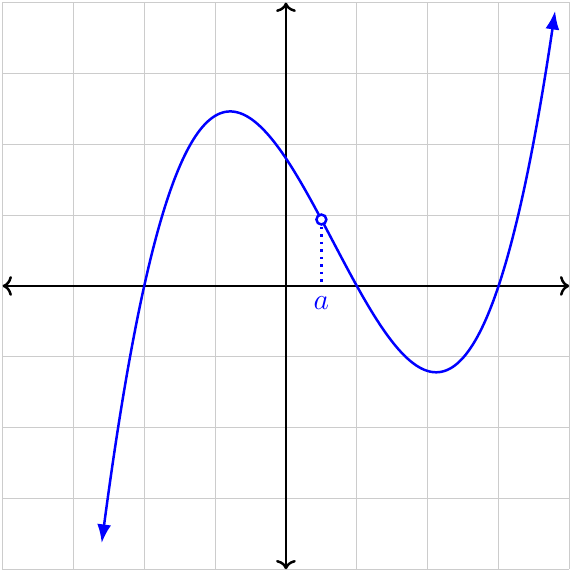
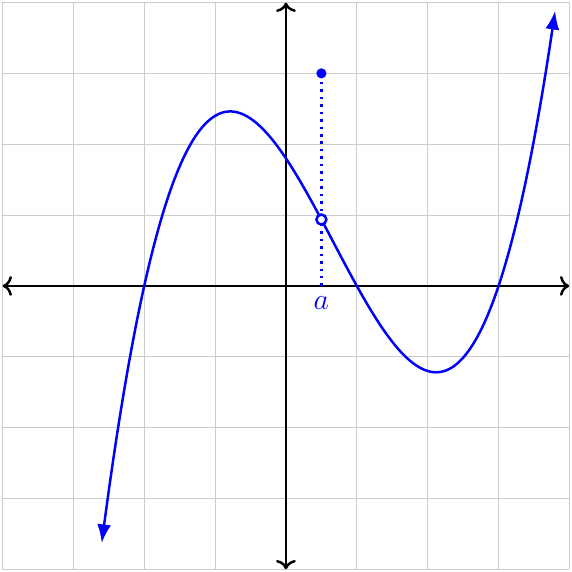
Continuity

A function \(f\) is said to be continuous at \(x=a\) if and only if

the function is defined at \(x=a\);
the limit as \(x\to a\) exists; and
the function value is equal to the limit.

Definition of continuity at \(a\)

\[f(a)=\lim\limits_{x\to a^-}f(x)=\lim\limits_{x\to a^+}f(x)\]

A function is said to be continuous over an interval \((a,b)\) if and only if it is continuous at every point in the interval.

A function is said to be continuous if and only if it is continuous at every point in its domain.

Types of discontinuities

If the function is undefined at \(x=a\), it is discontinuous at that point. The type of discontinuity depends on the limit as \(x\to a\). If the function is defined, it may still be discontinuous, also based on the limits.

Point (removable) discontinuity

The limit as \(x\to a\) exists and is finite, but the function value is not equal to the limit, or the function is undefined.

Jump discontinuity

The one-sided limits as \(x\to a\) exist and are finite, but they are not equal, so the limit does not exist.

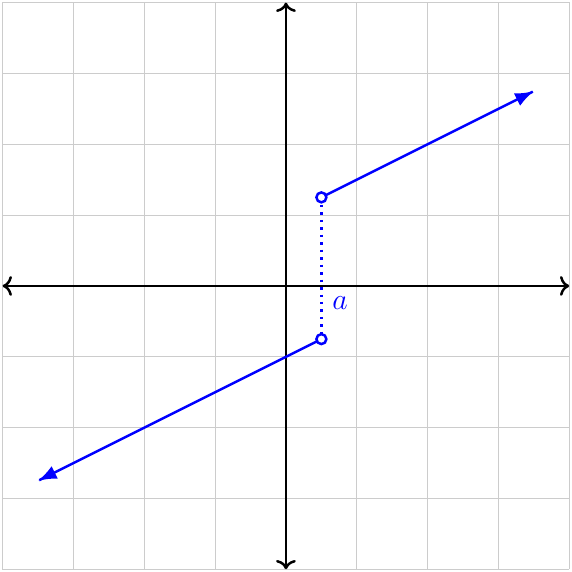
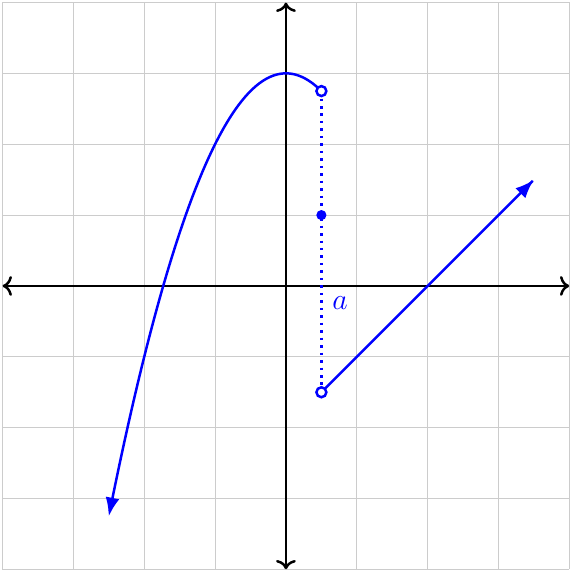
Asymptotic (infinite) discontinuity

Either (or both) of the one-sided limits as \(x\to a\) is (are) infinite, whether positive or negative.

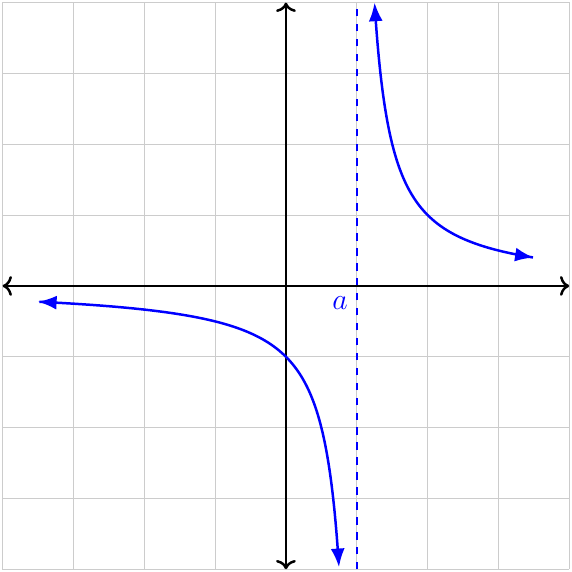
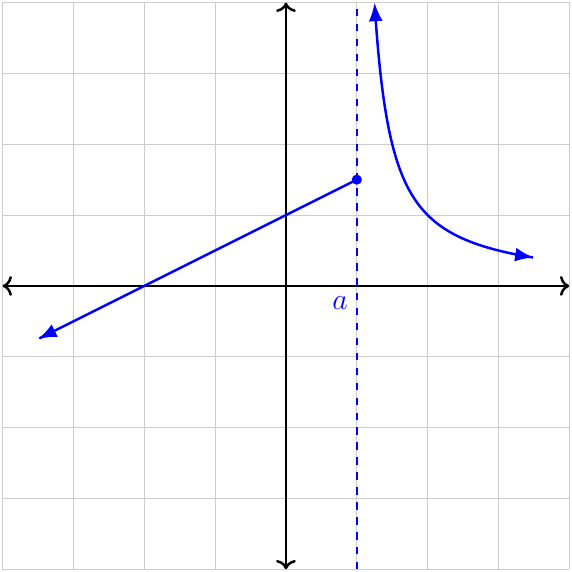
Essential discontinuity

Either (or both) of the one-sided limits does (do) not exist.